An inexact proximal algorithm for variational inequalities

Abstract

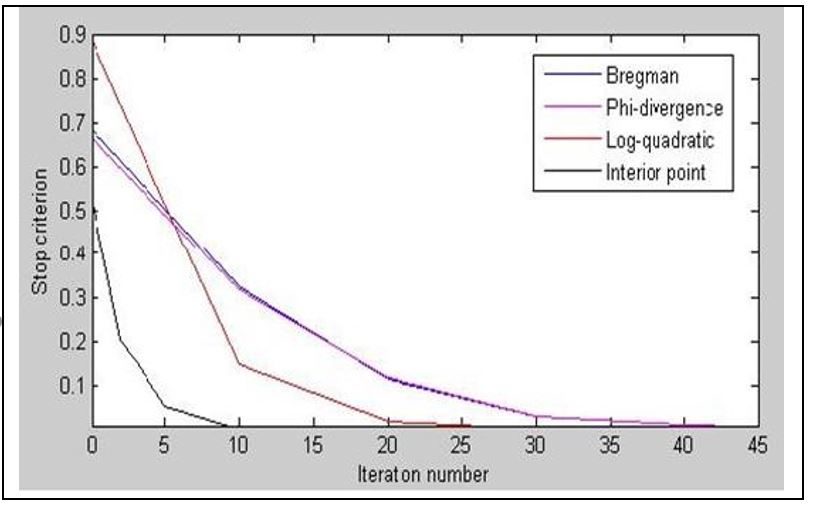
This paper presents a new inexact proximal method for solving monotone variational inequality problems with a given separable structure. The resulting method combines the recent proximal distances theory introduced by Auslender and Teboulle (2006) with a decomposition method given by Chen and Teboulle that was proposed to solve convex optimization problems. This method extends and generalizes proximal methods using Bregman, Phi-divergences and Quadratic logarithmic distances. Taking mild assumptions we prove that the primal-dual sequences produced by algorithm is well-defined and converge to optimal solution of the variational inequality problem. Furthermore, we show some numerical experiments, for the particular case to solve convex optimization problem, showing that the algorithm is perfectly implementable.