An inexact proximal algorithm for variational inequalities
DOI:
https://doi.org/10.33017/RevECIPeru2015.0018/Palabras clave:
Método proximal inexacto, desigualdad variacional, estructura separable, distancias proximalesResumen
En este artículo presentamos un nuevo método proximal inexacto para resolver problemas de desigualdad variacional monótono con una estructura separable. El método resultante combina la reciente teoria de distancias proximales introducidas por Auslender y Teboulle (2006) con un método de descomposición proximal dado por Chen y Teboulle que fue propuesto para resolver problemas de optimización convexa.
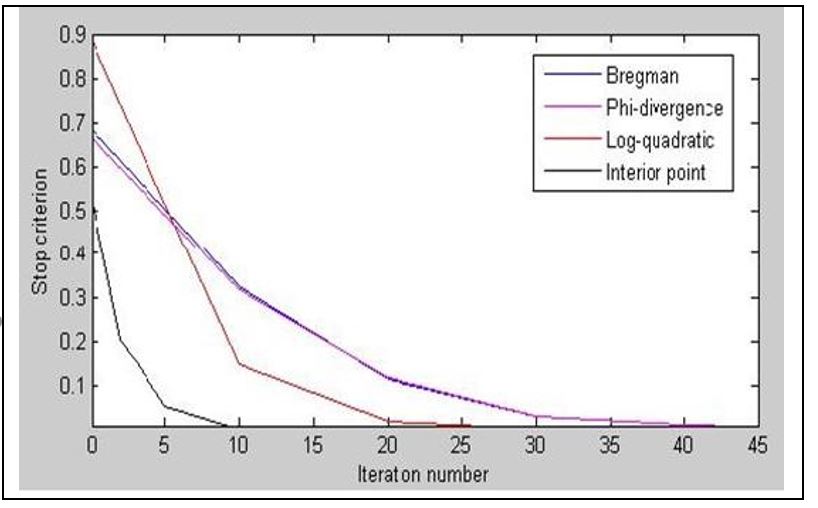
Este método extiende y generaliza métodos proximales usando distancias de Bregman, Phi-divergencias y logaritmo cuadrático, Asumiendo hipotesis adecuadas probamos que la sucesión primal-dual generada por el algoritmo está bien definido y converge a la solución óptima de un problema de desigualdad variacional. Además presentamos algunos resultados computacionales para el caso particular de resolver problemas de optimización convexa, mostrando asi que el algoritmo es perfectamente implementable.