MÉTODO DE DIFERENCIAS FINITAS PARA UN PROBLEMA DE VALOR DE FRONTERA UNIDIMENSIONAL
DOI:
https://doi.org/10.33017/RevECIPeru2006.0011/Palabras clave:
problema de valor de frontera unidimensional, diferencias finitas, matriz tridiagonal, método de Thomas, momento flexionante.Resumen
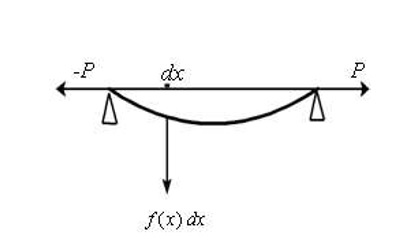
En este trabajo se considera el problema de valor de frontera unidimensional dado en (1). Se aproxima la solución del problema mediante el método de diferencias finitas suponiendo que la función c(x) es no negativa sobre 0,1, lo que permite establecer la convergencia del método de aproximación. El uso del método de diferencias finitas, a la vez, involucra la solución de sistemas de ecuaciones lineales con matrices muy ralas, cuyos ceros están posicionados de una manera remarcable. Dichas matrices son de tipo tridiagonal. Para la solución de dichos sistemas se ha utilizado el método de Thomas.